Wstęp
Rozpatrzmy takie zadanie: Mamy zestaw par punktów $\{x_i, y_i\}, i=0,1,2,\ldots,N$. Mogą pochodzić one z pomiarów jakiegoś zjawiska (z eksperymentu) albo z próbkowania jakiejś nieznanej funkcji $f(x)$: $(y_i=f(x_i)$). Nie znamy zależności pomiędzy $x$ a $y$ i poszukujemy takiej funkcji $w(x)$, że: $w(x_i)=y_i$.
Co więcej bardzo często żądamy dodatkowo, żeby funkcja pozwalała na łatwe manipulacje (dodawanie, mnożenie funkcji, różniczkowanie), a wyliczanie jej wartości nie było zbyt kosztowne.
Czasami zadanie stawiane jest niej ambitnie — mamy zestaw $\{x_i, y_i\}, i=0,1,2,\ldots,N$, a interesują nas wartości funkcji „między" tymi punktami.
W przypadku, gdy $A\le x_1 \le x_2 \le \cdots \le x_n \le B$, a interesują nas wartości funkcji dla argumentów $x<A$ lub $x>B$ (czyli spoza zakresu pomiarów) zadanie będziemy nazywać ekstrapolacją.
Wielomiany
Bardzo często jako funkcję $w(x)$ wybierane są wielomiany. Łatwo je różniczkować, stosunkowo łatwo obliczać wartość a i zadanie znalezienia współczynników wielomianu interpolacyjnego jest stosunkowo proste.
$$w_n(x)=\sum_{i=0}^{N} a_i x^i$$
Do wyliczania wartości takiego wielomianu najlepiej stosować schemat Hornera.
Interpolacja Lagrange’a
Interpolacja Lagrange’a polega na znalezieniu dla danego zestawu danych ${x_i, y_i}, i=0,1,2,\ldots,N$ wielomianu $W_n$ stopnia nie wyższego niż $n$, którego wartości w $n+1$ punktach $x_i$ są takie same jak wartości interpolowanej funkcji, tzn.:
$$W_n(x_i)=y_i, \quad \text{dla } i=0,1,2,\ldots,N$$
przy czym zakładamy, że gdy $i\ne j$ to $x_i \ne x_j$.
Można pokazać, że tak postawione zadanie interpolacyjne ma jednoznaczne rozwiązanie, które można przedstawić w postaci:
$$W_n(x)= \sum_{i=0}^N y_i l_i(x)$$
gdzie funkcja pomocnicza $l_i(x_j)=\delta_{ij}= \begin{cases} 1& \text{dla } i=j\\ 0& \text{dla } i\ne j \end{cases},$ w szczególności:
$$l_i(x)=\prod_{\substack{j=0\\j\ne i}}^N \frac{x-x_j}{x_i-x_j}$$Można pokazać że jest to jednoznaczne rozwiązanie problemu interpolacji Lagrange’a.
Niestety, postać Lagrange’a wielomianu interpolacyjnego jest bardzo niewygodna do prowadzenia jakichkolwiek obliczeń. Zazwyczaj wylicza się współczynniki wielomianu klasycznego i używa ich w obliczeniach.
Aby wyliczyć współczynniki wielomianu należy rozwiązać układ $n+1$ równań liniowych:
$$a_0+a_1x_+a_2 x_i^2+\cdots +a_N x_i^N = y_i, \quad i=0,1,\ldots,N$$
Z względu na specyficzną postać współczynników ($1, x, x^2,\ldots,x^N)$ — są one zależne, co może być problemem w przypadku równoodległych węzłów) najlepiej stosować specjalne metody rozwiązywania tego układu równań.
Jedna z nich, oparta na wyliczaniu ilorazów różnicowych opisana zostanie pokrótce niżej. Wspominam o niej z „konikarskiego obowiązku" — to właśnie do wyliczania wartości wielomianów interpolacyjnych Babbage budował swój pierwszy „komputer": Maszynę różnicową.
Wielomian interpolacyjny $W_n(x)$ zapisywany jest w alternatywnej postaci:
$$W_N(x) = \sum_{i=0}^N b_k p_k(x)$$
Wielomiany $p_k(x)$ opisane są wzorem:
$$\begin{split} p_0(x) & = 1\\ p_k(x) & = (x-x_0)(x-x_1)\ldots(x-x_{k-1}), \quad k=1,2,\ldots, N \end{split}$$Współczynniki $b_k$ dane są wzorem: $$b_k=\sum_{i=0}^k\frac{y_i}{\displaystyle\prod_{\substack{j=0\\j \ne i}}^k(x_i-x_j)}$$
Współczynniki $b_k$ noszą nazwę ilorazów różnicowych funkcji $f$ (pamiętamy, że $y_i=f(x_i)$) opartej na węzłach $x_0, x_1,\ldots,x_k$. Ilorazy różnicowe oznaczać będziemy tak: $f[x_l,x_{l+1},\ldots,x_{l+k}]$
$$f[x_l,x_{l+1},\ldots,x_{l+k}] = \sum_{i=l}^{l+k}\frac{y_i}{\displaystyle\prod_{\substack{j=l\\j \ne i}}^{l+k}(x_i-x_j)}$$Można pokazać, że zachodzi następująca zależność rekurencyjna: $$f[x_l,x_{l+1},\ldots,x_{l+k}]=\frac{f[x_{l+1},x_{l+2},\ldots, x_{l+k}] - f[x_{l},x_{l+1},\ldots, x_{l+k-1}]}{x_{l+k}-x_l}$$
Wyliczenie współczynników $b_k$ sprowadza się do rekurencyjnego wyliczania ilorazów różnicowych funkcji $f$. Budujemy tablicę zawierającą wartości $x_i$, wartości $f(x_i)$ oraz odpowiednie ilorazy różnicowe: $$\begin{array}{llllll} x_0 & f(x_0) \\ x_1 & f(x_1) & f[x_0,x_1] \\ x_2 & f(x_2) & f[x_1,x_2] & f[x_0,x_1,x_2] \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ %\hdotsfor{6}\\ x_n & f(x_n) & f[x_{n-1},x_n] & \ldots & \ldots & f[x_0,\ldots,x_n] %x_n & f(x_n) & f[x_{n-1},x_n] & \hdotsfor{1} & & f[x_0,\ldots,x_n] \end{array}$$ Szukane współczynniki $b_k$ równe są elementom przekątniowym powyższej tablicy.
Powyższe obliczenia można wykonać bardzo łatwo korzystając z następującego algorytmu:
for (k = 1; k <= n, k++)
for (l = n; l >= k; l--)
f[l] = (f[l] - f[l - 1]) / (x[l] - x[l - 1]);
Ponieważ najwygodniejszą (i najefektywniejszą) metodą liczenia wartości wielomianów jest metoda Hornera — trzeba korzystając ze współczynników $b_k$ wyliczyć współczynniki $a_i$ wielomianu w postaci naturalnej. Jest to również dosyć proste . Realizuje je następujący algorytm:
a[n] = b[n];
for (i = n - 1; i >= 0; i--)
{
xi = x[i];
a[i] = b[i];
for (k = i; k <= n - 1; k++)
a[k] = a[k] - xi * a[k + 1];
}
Naszkicowany powyżej algorytm jest praktycznie najefektywniejszym algorytmem interpolacji. Jedynie w przypadku interpolacji trygonometrycznej i użycia Szybkiej Transformaty Fouriera, dla dużych $N$ będzie ona tańsza od algorytmu ilorazów różnicowych. Zainteresowanie Babbage’a tym algorytmem nie powinno zatem budzić zdziwienia.
Przydatność algorytmu interpolacji pokazuje przykładowy notatnik Mathematici, gdzie na podstawie siedemnastu wartości funkcji sinus, które każdy zna (powinien znać) budowany jest wielomian interpolacyjny. Dla dużych $n$ (w tym wypadku 16) obliczenia chwilę trwają, ale wyniki są całkiem dokładne.
Funkcje sklejane
Interpolacja za pomocą wielomianów stopnia $n$, gdy $n$ jest duże ma szereg efektów ubocznych — gwarantuje co prawda, że $w_n(x_i) = f(x_i)$, ale nie gwarantuje żadnego „przyzwoitego zachowania pomiędzy węzłami. Im więcej punktów — tym wyższy stopień wielomianu i tym „gorzej" się on zachowuje.
Funkcję rzeczywistą $S$ nazywamy funkcją sklejaną stopnia $m$ z węzłami $a = x_0 < x_1 < \ldots < x_N = b$ jeśli
w każdym przedziale $(x_{i-1},x_i)$ dla $i = 0, 1, \ldots, N + 1$ $(x_{-1} = -\infty, x_{N+1} = \infty)$ $S$ jest wielomianem stopnia nie wyższego niż $m$,
$S$ i jej pochodne rzędu $1, 2, \ldots, m-1$ są ciągłe na całej osi rzeczywistej $S \in C^{m-1}$.
Gdy $m=1$, funkcja sklejana jest po prostu łamaną. Otrzymana funkcja interpolacyjna będzie ciągła, ale pochodna będzie nieciągła, co znaczy, że funkcja nie jest gładka. Można (podwyższając $m$) doprowadzić do sytuacje, że funkcja jest ciągłą, ma pochodną, która również jest ciągła. Otrzymana funkcja będzie gładka. (Natomiast może okazać się, że druga pochodna już ciągłą nie jest — co ma swoje konsekwencje.) Zazwyczaj ciągłość pierwszej, a czasami drugiej pochodnej jest wystarczająca.
Funkcje sklejane to specjalna kategoria funkcji interpolacyjnych. Są one skonstruowane z „kawałków" (funkcja może być inna w każdym przedziale interpolacji), ale mają szereg zalet. Nadają się zwłaszcza, gdy trzeba na podstawie siatki (na przykłąd MES) utworzyć gładką powierzchnię.
Szczególnym przypadkiem są krzywe Beziera (Bezier curve).
Mathematica
Interpolacja wielomianowa
Do wyliczania wielomianów interpolacyjnych służy funkcja Interpolation. Można jeż użyć albo tak:
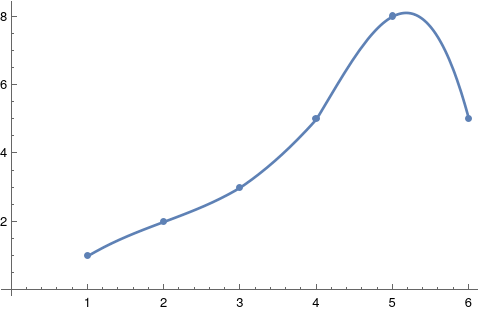
data = {1, 2, 3, 5, 8, 5};
f = Interpolation[data]
W tym przypadku zakłada się, że nasz zestaw danych to pary: ${(1,1)$, $(2,2)$, $3,3$, $(4,5)$, $(5,8)$, $(6,5)}$.
Rząd interpolacji wybierany jest automatycznie. Najlepiej gdyby rzad interpolacji był równy $n-1$ (gdzie $n$ to liczność zbioru danych). Gdy rząd jest mniejszy niż $n-1$ — interpolacja dokonywana jest za pomocą jakiejś formy funkcji sklejanych. W szczególności można zażądać, żeby użyta była metoda funkcji sklejanych dodając parametr Method$\to$"Spline".
Wynik interpolacji (w tym wypadku $f$) jest funkcją i może być używane tak jak każda funkcja:
f[2.5]
2.4375
Show[ListPlot[data], Plot[f[x], {x, 1, 6}]]
Gdy mamy zestaw danych pp, który jest tablicą dwuwymiarową zawierającą współrzędne węzłów w postaci $(x,y)$:
pp = {{0, 1}, {1/10, 2}, {1/5, -3}, {3/10, 5}, {2/5, 8}, {1/2, 3}}
ff = Interpolation[pp, InterpolationOrder -> 1];
Show[Plot[ff[x], {x, 0, 0.5}], ListPlot[pp, PlotStyle -> Red]]

Przykładowy notatnik Mathematici pokazujący zastosowanie interpolacji.
Interpolacja funkcjami sklejanymi
Do interpolacji funkcjami sklejanymi służyć mogą funkcje Interpolate lub ListInterpolate, gdy podamy jako metodę interpolacji "Spline". (W zasadzie nie widzę między nimi różnicy).
Przykładowy notatnik do porównania interpolacji wielomianowej i splajnów.
Matlab
Zakładam, że wszyscy Państwo znakomicie znacie Matlaba. Więc opisy są minimalne. Sugerują zabawy z Mathematicą.
Interpolacja wielominowa
Funkcja interp1 może być użyta do prostych zadań interpolacji. Korzysta z metod: ’nearest’, ’linear’,‘spline’,‘pchip’, or ‘cubic’ i nie interpoluje w sposób opisany w części teoretycznej.
Użycie:
vq = interp1(x, v, xq, method)
gdzie x tablica współrzędnych x węzłów interpolacji, v — tablica współrzędnych y węzłów, xq tablica zawierająca wartości punktów, w których chcemy wyliczyć wartości interpolowanej funkcji. Zakłada się, że węzły interpolacji są zapisane w kolejności rosnącej.
Istnieje również możliwość interpolacji na podstawie danych, które nie są w żaden sposób uporządkowane: na przykład mamy zestaw punktów w przestrzeni trójwymiarowej i chcemy narysować poziomice. Używa się wówczas metod opisanych jako interpolating scattered data.
Zadania
Przygotować przykład pokazujący zachowanie zachowanie wielomianu interpolacyjnego pomiędzy węzłami interpolacji.
Użyć interpolacji wielomianowej i za pomocą funkcji sklejanych do przebiegu temperatury z czujnika podczerwonego (plik ma w nazwie
temperatura_ir). W wyniku powinniśmy dostać dwa różne „przybliżenia" funkcji ale o tych samych wartościach w węzłach interpolacji. Należy policzyć pochodne obu funkcji interpolacyjnych. Wyniki porównać. Wyciągnąć wnioski. (Zamiast interpolacji wielomianowej — jeżeli trudno lub nie da się jej wyliczyć — można użyć jakiegoś innego sposobu interpolacji.)Hint: w przypadku Mathematici, aby uzyskać pochodną funkcji $f$ wystarczy napisać $f’$.
Sprawozdanie
Standardowe.
Lektury uzupełniające
Nieco teorii, ale inaczej podanej znaleźć można na blogu Szymona Wąsowicza: