Laboratorium 5: Szyfrowanie

Wprowadzenie

Jednym z pierwszych pomysłów na zapewnienie prywatności w sieci, było wprowadzenie szyfrowania.

Szyfrowanie stosowane było od wieków aby zapewnić prywatność przesyłania informacji. Jeżeli wierzyć przekazom — Juliusz Cezar (I w pne) używał stosunkowo prostego szyfru do kodowania informacji, które chciał ukryć.

Nie wchodząc w szczegóły, na przestrzeni wieków stosowano bardzo różne metody szyfrowania informacji. Były one zazwyczaj bardzo uciążliwe: Potrzebny był sposób na przekazanie (w odpowiednio zabezpieczony sposób) książki szyfrów lub hasła stosowanego w matematycznym procesie szyfrowania/deszyfrowania informacji.

Rewolucyjnym sposobem szyfrowania okazały się metoda szyfrowania asymetrycznego. Jej główne zasady są następujące:

Szyfrowania i deszyfrowanie wymagają innych kluczy.
Do zaszyfrowania wiadomości potrzebny jest jawny klucz odbiorcy¹.
Do odszyfrowania wiadomości potrzebny jest tajny klucz odbiorcy.

Metoda pozwala również podpisywać² wiadomości.

Do podpisania wiadomości potrzebny jest tajny klucz nadawcy.
Do sprawdzenia podpisu wystarczy jawny klucz nadawcy.

Najpopularniejszym algorytmem szyfrowania asymetrycznego jest algorytm RSA zaproponowany przez Rona Rivesta, Adiego Shamira oraz Leonarda Adlemana. Nazwa algorytmu pochodzi od pierwszych liter nazwisk twórców.

Algorytm został opatentowany przez MIT (autorzy byli pracownikami tej uczelni), mógł być wykorzystywany w celach niekomercyjnych, ale oprogramowanie powstałe na jego podstawie nie mogło być eksportowane ze Stanów Zjednoczonych bez zgody rządu (podobnie jak różne rodzaje broni).

Spowodowało to bardzo silny ruch sprzeciwu, a ponieważ algorytm został opublikowany w czasopiśmie naukowym, bardzo wielu ludzi (w latach dziewięćdziesiątych) nosiło podkoszulki z jego wydrukiem (patrz rysunek 1).

Dodatkowe informacje na temat szyfrowania znaleźć można na stronach MIMUW.

Wady szyfrowania asymetrycznego

Podstawową wadą szyfrowani asymetrycznego są spore wymagani obliczeniowe. W praktyce nie można go wykorzystywać na potrzeby szybkiej transmisji danych. W związku z tym, w takich zastosowaniach (HTTPS, TLS) używa się go tylko do przesłania klucza do prostszego symetrycznego algorytmu szyfrowania transmisji.

Funkcja skrótu

Do „podpisywania" różnych rzeczy potrzebne jest przekształcenie, które przypisze danym coś w rodzaju sumy kontrolnej (jak dane się zmienią — suma kontrolna powinna być inna). Przekształcenie to zwane jest funkcją skrótu (po angielsku hash function). Funkcja taka konwertuje dane o dowolnej długości do danych (podpisu, skrótu) o stałej długości. Dodatkowo, funkcja ta nie ma funkcji odwrotnej (na podstawie skrótu nie można odtworzyć danych wejściowych. Co więcej jest tak skonstruowana, że bardzo trudno jest stworzyć dwa różne zestawy danych wejściowych o tej samej wartości funkcji skrótu, ale nie jest to niemożliwe.

Przez wiele lat uważano algorytm MD5 (stworzony przez jednego z twórców RSA) za dobrą funkcję skrótu, ale powstały algorytmy pozwalające stosunkowo prosto znaleźć różne zestawy danych wejściowych posiadające tę samą wartość funkcji skrótu. Dziś używa się lepszych algorytmów (SHA-2, na przykład).

Cały czas jednak należy pamiętać, że jest tylko kwestią czasu (i mocy obliczeniowej) „złamanie" każdej takiej funkcji.

Rysunek 1: Fragmet podkoszulki z wydrukiem algorytmu RSA

Uświadomienie społeczeństwu, że istnieją nie tylko łatwe, ale też bardzo pewne metody szyfrowania rozpoczęło (w tamtych czasach) bardzo poważną dyskusję na temat prywatności komunikacji. NSA opracowała nawet specjalny układ scalony, który z jednej strony zapewniał prywatność komunikacji (ale tylko dla niewtajemniczonych) i nie zapewniał jej wobec agend rządowych. Układ nazywał się Clipper. Bardzo szybko został „rozpracowany", kodowanie zostało złamane. Układ był podatny na ataki siłowe (czyli „zgadywanie" haseł).

Zamysłem twórców było instalowanie go w aparatach telefonicznych (aby zapewnić ochronę przed podsłuchem).

Dosyć szybko idea tego układu upadła.

Algorytm RSA

Idea algorytmu RSA opiera się na znalezieniu dwu bardzo dużych³ liczb pierwszych.

Wybieramy losowo dwie duże liczby pierwsze $p$ i $q$.
Obliczamy ich iloczyn $n=pq$.
Obliczamy wartość funkcji Eulera dla $n: \varphi(n) = (p-1)(q-1)$
Wybieramy liczbę $e\quad 1 < e < \varphi(n)$ względnie pierwszą⁴ z $\varphi(n)$.
Znajdujemy taką liczbę $d$, że $de \equiv 1; (\mathrm{mod}, \varphi(n))$

Klucz publiczny to para liczb $(n, e)$, natomiast klucz prywatny to para liczb $(n, d)$.

Aby zaszyfrować wiadomość dzielimy ją na bloki $m$ o wartości liczbowej⁵ nie większej niż $n$. Każdy blok szyfrujemy według wzoru: $$c \equiv m^e; (\mathrm{mod}, n)$$ Każdemu blokowi $m$ odpowiada blok $c$, który jest przesyłany do odbiorcy.

Odszyfrowanie bloku polega na wykonaniu operacji „odwrotnej": $$m \equiv c^d; (\mathrm{mod}, n)$$

Podpisanie wiadomości polega na wyliczeniu funkcji skrótu dla wiadomości i zaszyfrowanie jej i dodaniu do przesyłanej wiadomości. Odbiorca odszyfrowuje wartość funkcji skrótu i porównuje ją z wyliczoną funkcją skrótu dla otrzymanej wiadomości.

Sam algorytm nie jest specjalnie ważny, zamieściłem go, by pokazać, że jest stosunkowo prosty. Jedyny kłopot to poradzenie sobie z operacjami arytmetycznymi (mnożenie, potęgowanie) wykonywanymi na bardzo dużych liczbach. Operacja modulo to najczęściej obcięcie nadmiarowych bitów wyniku (stąd klucze długości 1024, 2048,… — są to potęgi dwójki). Opracowano specjalne biblioteki matematyczne do wykonywania tych obliczeń.

PGP

PGP czyli Pretty Goog Privacy czyli „całkiem dobra prywatność" to narzędzie do szyfrowania poczty elektronicznej i zarządzania kluczami prywatywnymi i publicznymi, wykorzystujące algorytmy szyfrowania asymetrycznego.

Oprogramowanie opracowane przez Philipa Zimmermanna i dostępne początkowo na licencji otwartej, przekształcone później w biznes (co spowodowało powstanie równoważnego oprogramowania na licencjach otwartych).

Ponieważ eksport tego oprogramowania za granicę Stanów Zjednoczonych był nielegalny, wersja „europejska" powstałą na podstawie legalnie opublikowanej książki, legalnie wywiezionej ze Stanów Zjednoczonych z opublikowanym algorytmem. W którymś momencie Autor potwierdził „zgodność" europejskich algorytmów z wersją „oryginalną".

Instalacja

Parę uwag o instalacji, pod koniec instrukcji.

Mój klucz publiczny PGP

Rozpowszechnianie kluczy publicznych

Najsłabszą stroną szyfrowania niesymetrycznego jest sposób zaufanego rozpowszechniania kluczy publicznych.

Co z tego, że ktoś otrzyma wiadomość podpisaną przeze „mnie" (Wojciecha Myszkę), znajdzie gdzieś w Internecie „mój" klucz publiczny i stwierdzi, że wszystko się zgadza, skoro nie ma pewności, że ten klucz rzeczywiście należy do mnie?

W połowie lat dziewięćdziesiątych (gdy na topie były warianty systemu PGP) ludzie, którzy chcieli używać szyfrowania do wymiany korespondencji między sobą, organizowali key signing parties. Były to spotkania w realu, na których można było z rąk właściciela uzyskać jego klucz publiczny i dopisać go sobie do „kółka" (ang. keyring, czyli może raczej breloczka). Na spotkaniach tych można również było uzyskać „autograf" wielu znajomych osób potwierdzający, że ten klucz publiczny należy do…. Zwiększało to zaufanie do klucza publicznego osób które widzą że właściciel klucza i osoby które go podpisały są w „zażyłych" stosunkach (internetowych), czyli, na przykład, często ze sobą dyskutują na forach publicznych. System ten został nazwany „Siecią zaufania" (Web of Trust).

Tak podpisany klucz wysyłany był na serwer kluczy PGP⁶.

S/MIME

Gdy Internet zaczął się rozrastać sposób uwierzytelniania kluczy publicznych przyjęty dla PGP przestał wystarczać. Rozpoczęto tworzenie specjalnej infrastruktury zaufanych dostawców certyfikatów (czy może raczej dostawców podpisów certyfikatów). Nazywa się to PKI — Public Key Infrastructure.

S/MIME jest mechanizmem zbliżonym do PGP, ale opartym nie o „Web of Trust" tylko infrastrukturę PKI.

PKI

PKI czyli Public Key Infrastructure to cały system umożliwiający podpisywanie certyfikatów i sprawdzanie poprawności łańcucha podpisów.

W przypadku poczty elektronicznej chodzi o to, żeby można był zaufać programowi pocztowemu mówiącemu, że list został prawidłowo podpisany przez Wojciecha Myszkę. W związku z tym Wojciech Myszka ubiegając się odpowiedni certyfikat musi pojawić się osobiście w odpowiednim urzędzie wraz z dowodem osobistym (i wygenerowanym osobiście kluczem publicznym), gdzie jego klucz zostanie zarejestrowany, podpisany przez ten urząd i zwrócony do używania.

Każdy odbiorca listu podpisanego tak uzyskanym certyfikatem może w każdej chwili sprawdzić kto go wydał. Oprogramowanie (i PKI) dba o to, żeby być pewnym, że wszystkie podpisy są poprawne.

W przypadku mojego programu pocztowego wyglądało to jakoś tak jak przedstawiłem na rysunkach 2–4. Na wykazie listów elektronicznych, listy podpisane zaznaczone są kłódką (rys. 2). Po otwarciu listu (rys 3) pojawia się informacja, że jest on podpisany (signed) oraz dodatkowe informacje, że podpis jest poprawny i do kogo należy. Porównując nadawcę z tą informacją mam pewność, że wszystko jest OK. Mogę też sprawdzić szczegóły na temat wystawcy podpisu — rysunek 4.

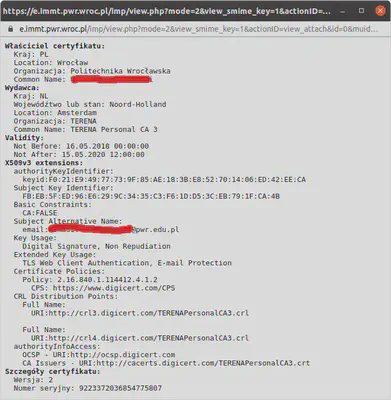
„Ścieżka" podpisów: Na dole Digicert, wyżej Terena — „Ścieżka” podpisów: Na dole Digicert, wyżej Terena

Najważniejsze jest sprawdzenie całej ścieżki zaczynającej się od podpisu listu pojedynczego nadawcy, który kończy się podpisem dobrze znanego urzędu certyfikacyjnego: list podpisał Pan Xiński, jego podpis podpisała Terena, podpis Tereny jest podpisany przez Digicert, który jest jedną z kilku firm znajdującą się na początku łańcucha certyfikacyjnego.

Praktycznie nikt nie wydaje darmowych osobistych certyfikatów (potwierdzających, że to Xiński wysłał list. Jest tylko jedna firma rozpowszechniająca darmowe certyfikaty związane z adresem e-mail (bo to się technicznie daje potwierdzić: na podany adres e-mail wysyłany jest kod, który trzeba przedstawić aby potwierdzić że jesteśmy właścicielami konta e-mail podczas zgłaszania prośby o certyfikat.

W przypadku stron WWW sprawa jest chyba szerzej znana, ale warto zwrócić uwagę na dwie różne sytuacje. Tu również certyfikat może potwierdzać, że połączyliśmy się ze stroną określonej instytucji (rys. 5) albo z określoną stroną (rys. 6). Te pierwsze są droższe. Te drugie można otrzymać nawet za darmo.

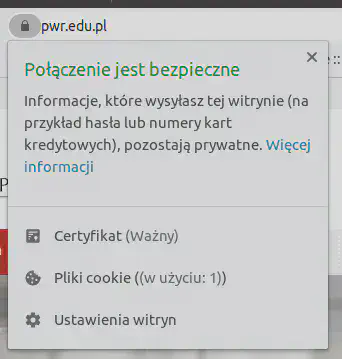
Certyfikat przyznany „adresowi strony" — Certyfikat przyznany „adresowi strony”

Aby doprowadzić do sytuacji, w której wszystkie (znakomita większość?) stron WWW korzystała z połączeń szyfrowanych powstałą inicjatywa (sponsorowane, między innymi, przez EFF, Mozillę, Internet Society).

Wszystkie instytucje wystawiające certyfikaty główne zrzeszone są w konsorcjum CA/Browser Forum dbającym o przestrzeganie dosyć restrykcyjnych zasad dotyczących infrastruktury, procedur bezpieczeństwa i procedur przyznawania certyfikatów.

Uwagi ogólne

Powszechna dostępność silnego szyfrowania stwarza problem wszystkim służbom specjalnym wszystkich rządów. Daje bowiem wszystkim (nie wyłączając „złych ludzi") narzędzie utrudniające inwigilację. Co jakiś czas pojawiają się (ze strony rządów i służb specjalnych) inicjatywy zmierzające do ograniczenia możliwości korzystania z szyfrowanego kanału przesyłania informacji. Wymienię tu niektóre:

Clipper (w czasach gdy pojawiło się PGP) rząd amerykański forsował instalowanie specjalnego układu szyfrującego, który miał zapewnić prywatność wobec sąsiadów, ale już nie służb⁷.
Blackberry firma ta, oferowała interesujące telefony używane (między innymi) przez biznesmenów. Głównym powodem ich popularności było dostarczanie narzędzi do szyfrowanej komunikacji. Komunikacja ta przechodziła przez serwery firm Blackberry (w Kanadzie) Rządy kilku państw (Rosja, Indie, Arabia Saudyjska,… o ile dobrze pamiętam) zabroniły korzystania z tych telefonów, chyba, że firma spowoduje, że „lokalna" komunikacja będzie przechodziła przez serwery ulokowane na ich terenie, a więc pod ich jurysdykcją.
NIST Narodowy Instytut Standaryzacji i Technologii to amerykańska agenda rządowa spełniająca rolę Głównego Urzędu Miar. Jednym z jej zadań jest podpowiadanie do stosowania standardów technologicznych.
Wybuchł skandal gdy okazało się, że po ogłoszeniu publicznego konkursu na algorytm szyfrowania (i opublikowaniu jego kodu, tak, żeby każdy kto zechce i potrafi mógł ocenić jego poprawność) zaimplementowano uproszczoną jego wersję istotnie osłabiającą szyfrowanie. Algorytm jednak był (i ciągle jest) stosowany przez wiele firm dostarczających sprzęt używany do komunikacji sieciowej.
EARN IT Na naszych oczach rozgrywa się batalia związana ze zgłoszonym do procedowania przez amerykańskich prawodawców aktem EARN IT⁸. Pretekstem do wprowadzenia tego prawa jest uniemożliwienie rozpowszechniania pornografii dziecięcej. Jest on tak sformułowany iż można traktować wszystkich, którzy zapewniają bezpieczny kanał komunikacji jako „działających lekkomyślnie". Warto przysłuchiwać się tej dyskusji.

Generacja kluczy

    gpg --gen-key
    gpg (GnuPG) 2.2.27; Copyright (C) 2021 Free Software Foundation, Inc.
    This is free software: you are free to change and redistribute it.
    There is NO WARRANTY, to the extent permitted by law.
    
    Uwaga: pełną funkcjonalność generowania klucza można uzyskać przez 
    ,,gpg --full-generate-key''.
    
    GnuPG musi utworzyć identyfikator użytkownika do identyfikacji 
    klucza.
    
    Imię i nazwisko: Imie Nazwisko
    Adres poczty elektronicznej: i.n@norka.eu.org
    Twój identyfikator użytkownika będzie wyglądał tak:
        "Imie Nazwisko <i.n@norka.eu.org>"
    
    Zmienić (I)mię/nazwisko, adres (E)mail, przejść (D)alej,
    czy (W)yjść z programu? D
    Musimy wygenerować dużo losowych bajtów. Dobrym pomysłem 
    aby pomóc komputerowi podczas generowania liczb pierwszych 
    jest wykonywanie w tym czasie innych działań (pisanie na klawiaturze, 
    poruszanie myszką, odwołanie się do dysków); dzięki temu 
    generator liczb losowych ma możliwość zebrania odpowiedniej ilości
    entropii.
    gpg: klucz 03C08E34F25D005A został oznaczony jako obdarzony 
    absolutnym zaufaniem.
    gpg: certyfikat unieważnienia został zapisany jako 
    ,,/home/myszka/.gnupg/openpgp-revocs.d/01E592B0C841352C7ED157C803C08E34F25D005A.rev''
    klucz publiczny i prywatny (tajny) zostały utworzone i podpisane.
    
    pub   rsa3072 2022-05-18 [SC] [wygasa: 2024-05-17]
          01E592B0C841352C7ED157C803C08E34F25D005A
    uid                      Imie Nazwisko <i.n@norka.eu.org>
    sub   rsa3072 2022-05-18 [E] [wygasa: 2024-05-17]

Generacja certyfikatu unieważnienia

Po utworzeniu pary kluczy został natychmiast wygenerowny certyfikat odwołania dla podstawowego klucza publicznego. Jeśli zapomnisz hasła lub jeśli klucz prywatny zostanie złamany lub utracony, ten certyfikat odwołania (revocation certificate) może zostać opublikowany w celu powiadomienia innych, że klucz publiczny nie powinien być dłużej używany.

Unieważnionego klucza publicznego można nadal używać do weryfikacji podpisów złożonych w przeszłości, ale nie można go używać do szyfrowania przyszłych wiadomości do Ciebie. Nie wpływa to również na możliwość odszyfrowania wiadomości wysłanych do Ciebie w przeszłości, jeśli nadal masz dostęp do klucza prywatnego.

Należy przenieść go na nośnik który można bezpiecznie ukryć; jeśli źli ludzie dostaną ten certyfikat w swoje ręce, mogą użyć go do uczynienia klucza nieużytecznym.

Niezłym pomysłem jest wydrukowanie certyfikatu unieważnienia i schowanie wydruku w bezpiecznym miejscu, na wypadek gdyby nośnik z certyfikatem stał się nieczytelny. Ale należy zachować ostrożność, systemy drukowania różnych komputerów mogą zachować treść wydruku i udostępnić ją osobom nieupoważnionym.

Listowanie kluczy

gpg --list-keys
/home/myszka/.gnupg/pubring.kbx
-------------------------------
pub   rsa3072 2020-03-24 [SC] [wygasa: 2023-05-14]
      50F967FE66E6841B420C1E6F6B396CE8C6A7790E
uid    [   absolutne   ] Wojciech Myszka <wojciech.myszka@pwr.edu.pl>
sub   rsa3072 2020-03-24 [E] [wygasa: 2023-05-14]

pub   rsa3072 2020-09-21 [SC] [wygasa: 2022-09-21]
      397071944EB1CC2F7C0B041772FE98A4157EF425
uid    [     pełne     ] r kk <218503@student.pwr.edu.pl>
sub   rsa3072 2020-09-21 [E] [wygasa: 2022-09-21]

pub   rsa3072 2021-05-13 [SC] [wygasa: 2023-05-13]
      0433B0B4C3AE49A010BF1A49970C534D99EB74CD
uid    [     pełne     ] Krzysztof Kempski <228985@student.pwr.edu.pl>
sub   rsa3072 2021-05-13 [E] [wygasa: 2023-05-13]

pub   rsa3072 2021-05-16 [SC] [wygasł: 2021-07-16]
      E6D8F5AAB01012DC3F47315FB7F1B714C03EAFBD
uid    [przeterminowany] Gabriel Maik <243742@student.pwr.edu.pl>

pub   dsa2048 2021-05-20 [SC]
      3B33B73BB13A0CAE021BA92E6ABE1B4F0F1AAED5
uid    [     pełne     ] majamex123@gmail.com <majamex123@gmail.com>
sub   elg2048 2021-05-20 [E]

pub   rsa3072 2022-05-18 [SC] [wygasa: 2024-05-17]
      01E592B0C841352C7ED157C803C08E34F25D005A
uid    [   absolutne   ] Imie Nazwisko <i.n@norka.eu.org>
sub   rsa3072 2022-05-18 [E] [wygasa: 2024-05-17]

Eksportowanie klucza publicznego

gpg --output alice.gpg --export alice@cyb.org

Zapisz klucz w postaci binarnej do pliku

gpg --armor --export alice@cyb.org

Zapisze klucz w postaci ascii

gpg --armor --export majamex123@gmail.com
-----BEGIN PGP PUBLIC KEY BLOCK-----

mQMuBGCmiiIRCACFoTGOP+239VO5wqApBnACutCWaa8HefXBeOjcn1+5FzqoaIiY
OfywMZU7sE10yNVDSJK0vzG1QLPTc5bDN/NZbQxoo7NDGN2YcNpkCrtcrGjom1aP
CaRkvdVRzedtlYnLhcTyPklMQwzG5b98UddX86p7gcY+ipiasF6/wU0JWqGlJs9U
KIIxQRU30O9bF1kjpjcvfCOIRWJncIqcmRv5rUK6PnOs8uZFokmCdzr1cS6hLZku
3cdJypDJDc+dhHhOE+FpKTbgL1bOacz64Ped937hkl+bFTnDzLUGv3Z72JzB8Z5k
...

Jak dodać --output klucz.asc zostanie zapisany do pliku o podanej nazwie (rozszerzenie asc jest powszechnie akceptowane przez inne oprogramowanie)

Importowanie klucza publicznego

gpg --import blake.gpg

Można od razu dodać dodatkowe informacje (na przykład podpisać go)

gpg a thunderbird

Dobry problem do rozważań.

Thunderbird obsługuje S/MIME
oraz
OpenPGP
gpg tp tylko OpenPGP (choć…)
Gdy wygenerujemy klucz PGP w thunderbirdzie nie będzie on widoczny dla gpg
I odwrotnie — klucze gpg nie są widoczne dla thunderbirda.
Światy są równoległe.

W pewnym sensie może wygodniejsze być wygenerowanie klucza w gpg i import do thunderbirda: dostaniemy wszystkie możliwości (szyfrowanie plików) plus możliwość wysyłania poczty.

Odwrotne postępowanie jest również możliwe, ale wydaje mi się mniej wygodne.

Import klucza gpg do thunderbirda

Trzeba własny klucz prywatny wyeksportować do postaci ascii

gpg --export-secret-keys --armor > my-secret-keys.asc

i plik my-secret-keys.asc zaimportować w thunderbirdzie oraz powiedzieć programowi, żeby go używał.

Zadania do wykonania

Zainstalować oprogramowanie OpenPGP.
- dla Windows może to być Gpg4win,
- dla linuksa gpg (będące standardowym pakietem we wszystkich dystrybucjach)
Wygenerować klucze, trzeba będzie podać imię i nazwisko oraz adres e-mail.
Stworzyć plik tekstowy, podpisać go, sprawdzić podpis, a następnie zmodyfikować⁹ go i sprawdzić podpis. System powinien pokazać, że plik został zmieniony. Dodatkowe wyjaśnienia na osobnej stronie.
Wymienić się (z innymi uczestni(cz)kami kursu kluczami publicznymi i wymienić podpisanymi plikami. Sprawdzić ich autentyczność. Możecie też Państwo przesłać klucze publiczne do mnie z prośbą o ich podpisanie. Podpiszę i odeślę¹⁰.
Zaszyfrować plik i przesłać do wybranego odbiorcy (z grupy). Rozszyfrować plik otrzymany od kolegi/koleżanki.
Spróbować skorzystać z jakiegoś narzędzia do wysyłania poczty z użyciem PGP. Listy dostępnych narzędzi znaleźć można tu:

Kolejne uwagi techniczne…

…które być może nie są oczywiste.

Przed podpisaniem/zaszyfrowaniem plik jest kompresowany. Kompresja (bezstratna) likwiduje nadmiarową entropię z wiadomości utrudniając wykonywanie prostych analiz statystycznych.
Z powyższego względu podpisany plik jest plikiem binarnym.
Stwarza to pewne problemy podczas rozsyłania poczty elektronicznej.
Można więc podpisać plik tak, aby nadawał się do wysłania pocztą elektroniczną (ale tu trzeba być bardzo ostrożnym, niektóre programy pocztowe przerabiają tekst na HTML i nawet jeżeli wygląda on identycznie u odbiorcy — tekstowo to zupełni inna zawartość).
Podpisany plik (w formacie tekstowym) wyglądać może tak jak na rysunku 7.
W przypadku podpisanej poczty jest ona wysyłana w taki sposób, żeby klient poczty nie rozumiejący szyfrowania mógł również list odczytać. Gdy list jest zaszyfrowany, odczytanie go bez oprogramowania rozumiejącego szyfrowanie będzie to niemożliwe.
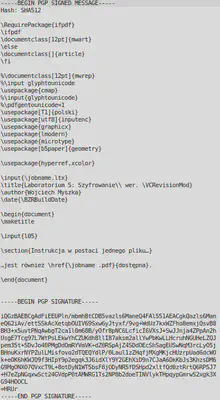
Podpisany plik tekstowy

Podpisanie pliku, sprawdzenie podpisu

Otrzymałem pytanie jak wykonać punkt 8.3 „Stworzyć plik tekstowy, podpisać go, sprawdzić podpis, a następnie zmodyfikować go i sprawdzić podpis. System powinien pokazać, że plik został zmieniony."

Ja tu będę używał bezpośrednio poleceń oprogramowania gpg (nie używając żadnego środowiska graficznego).

Tworzę plik o nazwie ala.txt zawierający tekst Ala ma kota.
Podpisuję ten plik używając polecenia gpg --output ala.txt.sig --sign ala.txt. Program pyta o hasło odbezpieczające klucz i robi swoje.
Utworzony jest plik (binarny) ala.txt.sig. Trudno go obejrzeć, ale w systemie Linux jest znakomity edytor nazywający się vim. Pozwala zajrzeć do każdego pliku. Plik wygląda tak:
Jak widać jest tam zakodowana zarówno pierwotna nazwa pliku, jak i jego zawartość. Całą reszta to binarny (ustandaryzowany) pojemnik zawierający dodatkowo podpis pliku. Nie jest to format wygodny do użytku.

Znacznie lepiej jest podpisać ten dokument w sposób pozwalający na odczyt jego zawartości nawet bez specjalnego oprogramowania. Robi się to poleceniem: gpg --clearsign ala.txt. Program utworzy plik o nazwie ala.txt.asc i zawartości:

Składa się on z dwu części: tekstu wiadomości i podpisu. Bez specjalnego oprogramowania można przeczytać wiadomość. Można też sprawdzić jej poprawność poleceniem gpg --verify ala.txt.asc. Efekt pracy gpg jest taki:

gpg: Podpisano w pon, 20 kwi 2020, 11:06:45 CEST
gpg:                przy użyciu klucza RSA 50F967FE66E6841B420C1E6F6B396CE8C6A7790E
gpg: Poprawny podpis złożony przez ,,Wojciech Myszka <wojciech.myszka@pwr.edu.pl>'' [absolutne]

Teraz plik ala.txt.asc zmodyfikuję zamieniając wielkie A na małe:

-----BEGIN PGP SIGNED MESSAGE-----
Hash: SHA512

ala ma kota
-----BEGIN PGP SIGNATURE-----

iQGzBAEBCgAdFiEEUPln/mbmhBtCDB5vazls6ManeQ4FAl6dZiUACgkQazls6Man
…

Próba weryfikacji takiego pliku kończy się komunikatem:

gpg: Podpisano w pon, 20 kwi 2020, 11:06:45 CEST
gpg: przy użyciu klucza RSA 50F967FE66E6841B420C1E6F6B396CE8C6A7790E
gpg: NIEPOPRAWNY podpis złożony przez 
gpg: ,,Wojciech Myszka <wojciech.myszka@pwr.edu.pl>'' [absolutne]

co należy rozumieć, że zawartość pliku została zmieniona.

Aby odzyskać pierwotną zawartość z pliku podpisanego należy użyć opcji --decrypt: gpg --decrypt ala.txt.sig; zawartość zostanie wypisana na terminalu, ale dodanie --output zapisuje do pliku: gpg --output ala --decrypt ala.txt.sig. Za każdym razem program informuje o poprawności podpisu. Nawet gdy podpis jest niepoprawny zawartość zostanie „odtworzona"¹¹.

W przypadku gdy modyfikacji ulegnie podpis, komunikat programu gpg może wyglądać tak:

gpg: Błąd sumy CRC; 670360 - 7656D9
gpg: [don't know]: invalid packet (ctb=21)
gpg: nie znaleziono podpisu
gpg: nie można sprawdzić podpisu.
Należy pamiętać o podawaniu pliku podpisu (.sig lub .asc) 
jako pierwszego argumentu linii poleceń.

Szyfrowana poczta

Najnowsza wersja programu thunderbird pooosiada już wbudowaną możliwość szyfrowania z użyciemm OpenPGP i/lub S/MIME. Nie są potrzebne żadne dodatkowe programy.

Wystarczy podczas konfiguracji programu skonfgurować opcję „Szyfrowanie „end-to-end" (rys. 8, 9).

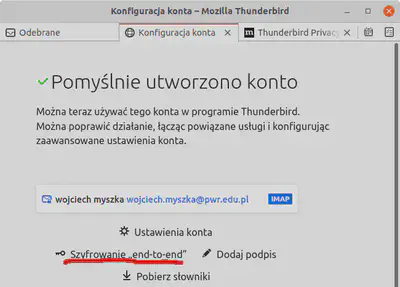
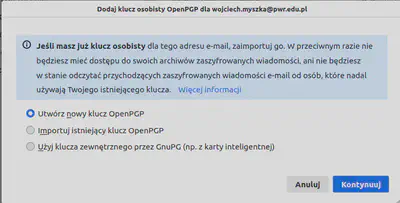
Nie ma więc potrzeby tworzenia specjalnego kanału na przesłanie jakiegoś tajnego klucza. ↩︎
Wiadomość podpisana, to taka wiadomość co do której można mieć pewność, że nie została zmodyfikowana podczas transmisji oraz (w określonych warunkach) pewność, że została wysłana przez tego, kto jest wpisany jako jej nadawca. ↩︎
Trudno powiedzieć co to znaczy „bardzo duża" liczba. W zapisie binarnym liczba o długości 768 bitów (to znaczy rzędu $2^{768}$, czyli nieco więcej niż 230 cyfr dziesiętnych) nie jest już uważana za liczbę bardzo dużą. Udało się złamać klucz o takiej długości. Klucze o długości większej niż 1024 są (na razie) uważane za bezpieczne. ↩︎
Czyli taką, że jedynym wspólnym dzielnikiem obu liczb jest 1. ↩︎
Wiadomość traktowana jest jako ciąg bitów, któremu można przypisać wartość liczbową/ ↩︎
Kilka takich serwerów ciągle działa i można tam znaleźć mój klucz publiczny pochodzący z sierpnia 1995 roku… Inna rzecz, że z powodu zmian oprogramowania mam ograniczone możliwości skorzystania z klucza prywatnego stworzonego gdzieś w sierpniu 1995 roku. ↩︎
Ponieważ oferował słabszą wersję szyfrowania, mogła być ona złamana również przez innych „złych ludzi". ↩︎
Tłumaczy się to na Eliminating Abusive and Rampant Neglect of Interactive Technologies (EARN IT). ↩︎
Na przykład dodać lub usunąć jedną spację. ↩︎
Niekoniecznie jest to najlepsza metoda — bo ktoś się może podszyć, ale w warunkach odosobnienia… Chyba, że je zlikwidują, to zrobimy to na zajęciach laboratoryjnych. ↩︎
Gdy podpis jest niepoprawny — zostanie odtworzona zmodyfikowana wersja pliku. Po modyfikacji podpisu zostanie odtworzona zawartość pliku (ale nie będziemy w stanie nic na jej temat powiedzieć). ↩︎